ما هي الأعداد الأولية؟

Meriem نوفمبر 19, 2022

0 25 8 دقائق

هل تساءلت يومًا عن ماهية الأعداد الأولية وطريقة استعمالها؟ فلنعد بالتاريخ قليلًا إلى الوراء لنتعرف على مكتشفها ومتى استخدمت لأول مرة.

1/n
Why are mathematicians interested in the distribution of prime numbers, and what do they actually mean by that?
A 🧵 on the Riemann hypothesis and Yitang Zhang's latest preprint on the Landau-Siegel zeros conjecture, which I covered yesterdayhttps://t.co/PCua3EKpFD
— Davide Castelvecchi (@dcastelvecchi) November 12, 2022

تشير بعض السجلات التاريخية العتيقة إلى أن المصريين القدماء هم أول من وضع مفهوم الأعداد الأولية، حيث يأخذ التحليل إلى كسر مصري شكلا مختلفا عندما يطبق على أعداد أولية عن الشكل الذي يأخذه عندما يطبق على أعداد غير أولية.

ومع ذلك، يظل اليونانيون القدامى أول من أجرى دراسات جدية حول الأعداد الأولية. حيث قام عالم الرياضيات اليوناني إراتوستينس بدراسة الأعداد الأولية. ورغم أن أي من مخطوطاته لم يعثر عليها، فقد أشار إليها علماء آخرون.

محتوى المقال

ما هي الأعداد الأولية؟

الأعداد الأولية هي تلك التي تقبل القسمة على عددين فقط وهما: 1 والعدد نفسه. فعلى سبيل المثال، الرقم 5 يقبل القسمة على 1 و 5 فقط، مما يعني أنه عدد أولي.

بالمقابل، الرقم 6 يقبل القسمة على أكثر من عددين (1 و 2 و 3 و 6)، مما يعني أنه عدد غير أولي. الرقم 1 هو حالة خاصة، فهو يقبل القسمة على عدد واحد فقط. لذلك، لا يعتبر عددًا أوليًا لأن العدد الأولي يقبل القسمة على عددين بالضبط. هذا يعني أن 1 ليس عددًا أوليًا ولا رقمًا مركبًا، إنه رقم فريد.

قائمة الأعداد الأولية:

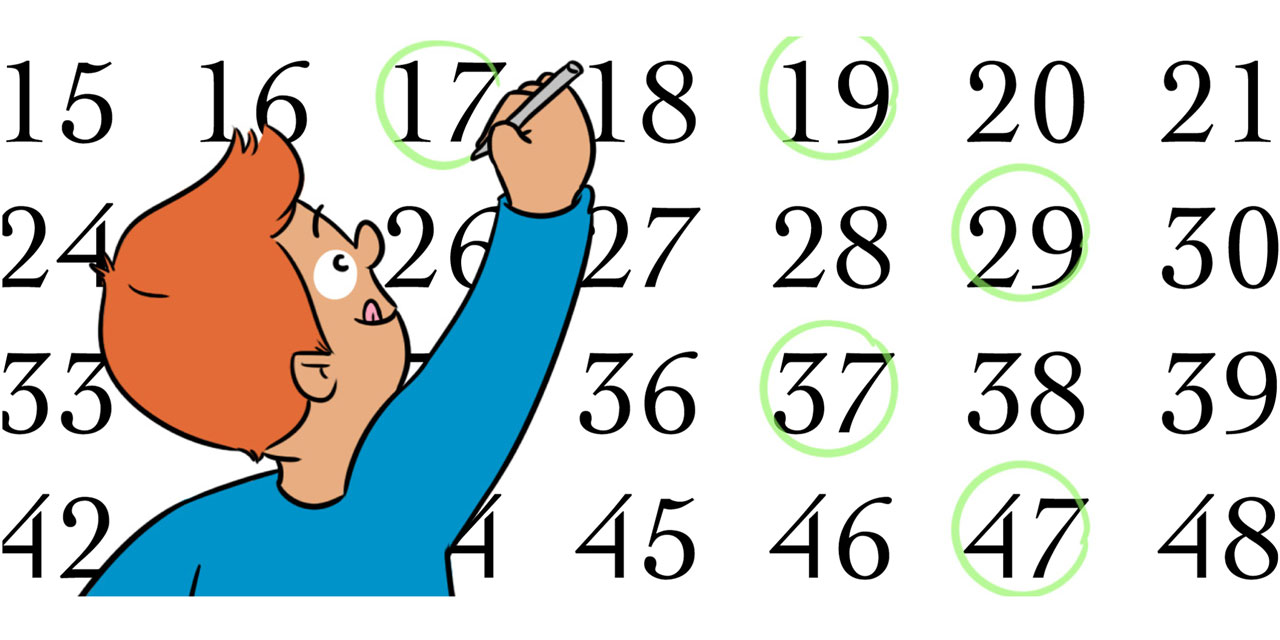
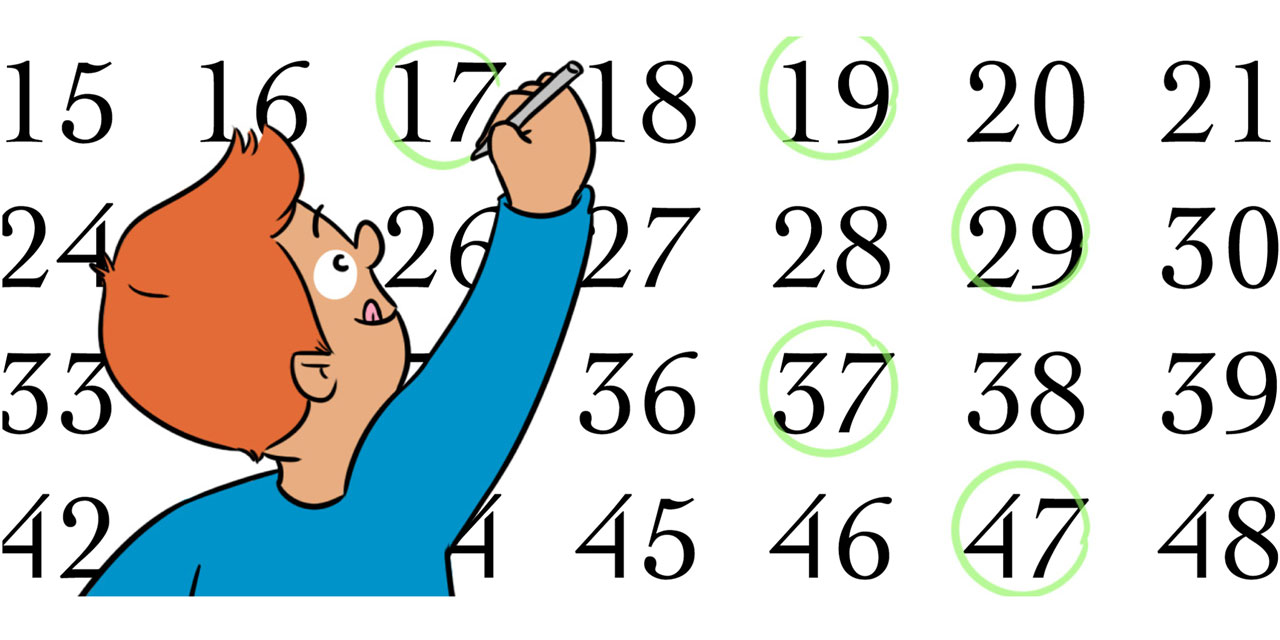
يوجد 25 عددًا أوليًا من 1 إلى 100. إليك القائمة الكاملة للأعداد الأولية من 1 إلى 100 أدناه:

بين 1 و 10: 2، 3، 5، 7.
بين 11 و 20: 11، 13، 17، 19.
بين 21 و 30: 23، 29.
بين 31 و 40: 31، 37.
بين 41 و 50: 41، 43، 47.
بين 51 و 100: 53، 59، 61، 67، 71، 73، 79، 83، 89، 97.

خصائص الأعداد الأولية:

فيما يلي بعض الخصائص المهمة للأعداد الأولية:

العدد الأولي هو عدد صحيح أكبر من 1.
يقبل القسمة على عددين بالضبط، أي 1 والرقم نفسه.
يوجد عدد أولي زوجي واحد فقط وهو 2.
أي عددين أوليين يكونان دائمًا أوليين لبعضهما البعض.
يمكن التعبير عن كل رقم على أنه حاصل ضرب الأعداد الأولية.
الأعداد الأولية تكون غير منتظمة في ترتيبها أو توزيعها وذلك بسبب أن العلماء لم يكتشفوا بعد طريقة توزيع الأعداد الأولية.
كلما زادت قيمة العدد الأولي كلما زادت الفجوة أو الأعداد التى توجد بيته وبين العدد الأولي الذي يليه في الترتيب.
كل الأعداد التي تنتهي بأحد الأرقام التالية: 1 و 3 و 7 و 2 هي أعداد أولية. ‏ويستثنى من تلك القاعدة العددان 2 و 5 ويرجع السبب في ذلك أن الأعداد التى تنتهي بالعدد 0 والعدد‎ ‏2 والعدد 4 والعدد 6 والعدد 8 تعتبر من مضاعفات 2، لذا فهي أعداد غير أولية. كما أن الأعداد التي تنتهي بالعدد 0 والعدد 5 تعتبر من مضاعفات العدد 5 وبالتالي هي ليست أعداد أولية.‎

اقرأ أيضًا: طريقة سهلة لحفظ جدول الضرب

الأعداد الأولية وغير الأولية:

العدد الأولي هو كل عدد أكبر من 1 يقبل القسمة على عددين بالضبط، بينما يقبل العدد غير الأولي القسمة على أكثر من عاملين. على سبيل المثال، يمكن تحليل 5 بطريقة واحدة فقط، أي 1 × 5 أو 5 × 1. مما يعني أن لديه عاملين فقط، وهما 1 و 5. لذلك، 5 هو عدد أولي.

العدد غير الأولي هو كل عدد أكبر من 1 ويقبل القسمة على أكثر من عددين. فعلى سبيل المثال، يمكن تحليل الرقم 4 بعدة طرق، فهو يقبل القسمة على كل من 1 و 2 و 4. ولذلك، يُصنف على أنه عدد غير أولي.

دعونا نفهم الفرق بين الأعداد الأولية وغير الأولية بمساعدة الجدول الوارد أدناه:

الأعداد الأولية	الأعداد غير الأولية
أعداد أكبر من 1 تقبل القسمة على عددين فقط، 1 والرقم نفسه	أعداد أكبر من 1 تقبل القسمة على ثلاثة أعداد على الأقل
2 هو الأصغر والرقم الأولي الزوجي الوحيد	4 هو أصغر عدد غير أولي
أمثلة على الأعداد الأولية: 2، 3، 5، 7، 11، 13….	أمثلة على الأعداد غير الأولية: 4، 6، 8، 9، 10..

الأعداد الأولية والأعداد الأولية فيما بينها:

هناك فرق بين الأعداد الأولية والأعداد الأولية فيما بينها. تسرد النقاط التالية الفرق بين الأعداد الأولية والأعداد الأولية فيما بينها:

تأتي الأعداد الأولية المشتركة دائمًا في صورة أزواج، بينما الرقم الأولي هو عدد واحد فقط.
إذا لم يكن لزوج من الأرقام عامل مشترك بصرف النظر عن 1، فإن هذه الأعداد تسمى أعداد أولية فيما بينها. الأعداد الأولية ليس لها أي شرط من هذا القبيل.
يمكن أن تكون الأعداد أولية فيما بينها عندما يكون القاسم المشترك الأكبر هو دائمًا 1.

أمثلة عن الأعداد الأولية فيما بينها:

5 و 9 أوليان فيما بينهما، حيث أن قواسم 5 هي 1 و 5؛ وقواسم 9 هي 1 و 3 و 9. نلاحظ أن لهذه الأعداد قاسم مشترك أكبر وحيد وهو 1، وبالتالي، فهما عددان أوليان فيما بينهما.
6 و 11 أوليان فيما بينهما، حيث أن قواسم 11 هي 1 و 11؛ وقواسم 6 هي 1 و 2 و 3 و 6. نلاحظ أن لهذه الأعداد قاسم مشترك أكبر وحيد وهو 1، وبالتالي، فهما عددان أوليان فيما بينهما.
18 و 35 أوليان فيما بينهما، حيث أن قواسم 18 هي 1 و 2 و 3 و 6 و 9 و 18؛ وقواسم 35 هي 1 و 5 و 7 و 35. نلاحظ أن لهذه الأعداد قاسم مشترك أكبر وحيد وهو 1، وبالتالي، فهما عددان أوليان فيما بينهما.
تجدر الإشارة إلى أن الأعداد الأولية فيما بينها ليست بالضرورة أعدادًا أولية.

طريقة سهلة للعثور على الأرقام الأولية:

هناك طرق مختلفة لإيجاد الأعداد الأولية، فلنتعرف على اثنين من هذه الأساليب:

الطريقة 1:

استبدل الأعداد الصحيحة بـ n في الصيغة ‘n2 + n + 41’. ستعطيك هذه الصيغة جميع الأعداد الأولية الأكبر من 40. إليك بعض الأمثلة:

الرقم 0: 0² + 0 + 41 = 0 + 41 = 41
الرقم 1: 1² + 1 + 41 = 2 + 41 = 43
الرقم 2: 2² + 2 + 41 = 6 + 41 = 47

الطريقة 2:

يمكن العثور على كل عدد أولي، باستثناء 2 و 3، باستخدام الصيغة: “6n + 1 أو 6n – 1” عن طريق استبدال الأعداد الصحيحة بـ n. إليك بعض الأمثلة:

دعونا نتحقق من صيغة 6n – 1 للرقم 1: 6 (1) – 1 = 5. إذن، 5 عدد أولي.
دعونا نتحقق من صيغة 6n + 1 للرقم 1: 6 (1) + 1 = 7. إذن، 7 عدد أولي.
دعونا نتحقق من صيغة 6n – 1 للرقم 2: 6 (2) – 1 = 11. إذن، 11 عدد أولي.
دعونا نتحقق من صيغة 6n + 1 للرقم 2: 6 (2) + 1 = 13. إذن، 13 عدد أولي.

قائمة الأرقام الأولية الفردية:

مخطط الأرقام الأولية هو مخطط يعرض قائمة الأعداد الأولية بترتيب منتظم. وتجدر الإشارة إلى أن جميع الأعداد الأولية هي أعداد فردية باستثناء الرقم 2 وهو عدد زوجي. ومن المثير للاهتمام أن 2 هو العدد الأولي الوحيد الذي هو زوجي، هذا يعني أن قائمة الأعداد الفردية يمكن أن تبدأ من 3 فصاعدًا وتستمر لأن باقي الأعداد الأولية هي أعداد فردية. على سبيل المثال، 3 و 5 و 7 و 11 و 13 و 17 و 19 و 23 و 29 و 31 و 37 و 41 و 43 و 47 و 53 و 59 و 61 و 67 و 71 و 73 و 79 و 83 و 89 وهكذا دواليك هي أعداد أولية فردية.

تاريخ الأعداد الأولية:

خلقت الأعداد الأولية فضول الإنسان منذ العصور القديمة. وحتى اليوم، يحاول علماء الرياضيات إيجاد الأعداد الأولية ذات الخصائص الغريبة.

أول عالم اقترح نظرية حول الأعداد الأولية كان العالم الإغريقي إقليدس، وتنص نظريته على أنه يوجد عدد لا نهائي من الأعداد الأولية.

بعد إقليدس، جاء الدور على إراتوستينس والذي كان أحد أعظم العلماء الذين عاشوا بعد عقود قليلة من إقليدس. حيث صمم طريقة ذكية لتحديد جميع الأعداد الأولية حتى رقم معين، هذه الطريقة تسمى غربال إراتوستينس. دعونا نتعرف عليها:

غربال إراتوستينس:

غربال إراتوستينس هو خوارزمية قديمة تساعد في إيجاد الأعداد الأولية إلى أي حد معين. يوضح الشكل التالي الأعداد الأولية حتى 100 التي تم العثور عليها باستخدام غربال إراتوستينس، حيث تمثل الأرقام غير المتقاطعة في الشكل الأعداد الأولية المتبقية بعد استخدام هذه الطريقة.

لنفترض أننا بحاجة إلى إيجاد الأعداد الأولية حتى ‘n’، لذلك سننشئ قائمة بجميع الأعداد من 2 إلى n. توضح الخطوات التالية كيفية إيجاد جميع الأعداد الأولية حتى 100 باستخدام غربال إراتوستينس.

الخطوة 1:

قم أولاً بإنشاء قائمة بالأرقام من 2 إلى 100 كما هو موضح أعلاه. نترك الرقم 1 لأن جميع الأعداد الأولية أكبر من 1.

الخطوة 2:

نبدأ من الرقم 2 الأول في القائمة. نقوم بشطب كل رقم يكون من مضاعفات 2 باستثناء 2. على سبيل المثال، نشطب 4 و 6 و 8 و 10 و 12 و 14 و 16 وهكذا حتى 100.

الخطوة 3:

بعد ذلك، ننتقل إلى الرقم التالي غير المشطوب وهو 3، ثم نقوم بشطب كل رقم مضاعف للعدد 3 باستثناء 3. وسيشمل هذا عددًا قليلاً من المضاعفات التي تم شطبها بالفعل. لذلك نواصل عملية شطب باقي المضاعفات غير المشطوبة. على سبيل المثال: 9، 15، 21 وهكذا حتى 100.

الخطوة 4:

بعد ذلك، ننتقل إلى الرقم غير المشطوب التالي في القائمة بعد 3 وهو 5. نشطب كل عدد مضاعف للعدد 5 باستثناء الرقم 5. وسيشمل هذا عددًا قليلاً من المضاعفات التي تم شطبها بالفعل. لذلك سنقوم بشطب الأعداد المتبقية، على سبيل المثال، 25، 35، 55 وهكذا حتى 100.

الخطوة 5:

7 هي الرقم التالي غير المشطوب في القائمة بعد 5. لذا، نشطب كل عدد مضاعف لـ7 باستثناء 7. وسيشمل هذا عددًا قليلاً من المضاعفات التي تم شطبها بالفعل. على سبيل المثال 49.

بعد هذه الخطوة، لن تبقى إلا الأعداد الأولية فقط. فباستعمال غربال إراتوستينس، قمنا بتشطب جميع الأعداد ولم يتبقى سوى الأعداد الأولية.

أصغر عدد أولي:

أصغر عدد أولي هو 2. ومن المثير للاهتمام أنه أيضًا العدد الزوجي الوحيد الذي يمثل عددًا أوليًا. تجدر الإشارة إلى أن 1 ليس عددًا أوليًا ولا عددًا غير أولي لأنه يقبل القسمة على عامل واحد فقط وهو 1، وبالتالي فهو رقم فريد.

الأعداد الأولية الزوجية:

كما ذكرنا سابقًا، العدد الأولي الوحيد الذي هو عدد زوجي هو 2. وهذا يعني أن جميع الأعداد الزوجية هي أعداد غير أولية. 2 يعتبر عددًا أوليًا لأنه يقبل القسمة على عاملين 1 والرقم 2 نفسه.

أكبر عدد أولي:

لا يمكن العثور على أكبر عدد أولي لأن الأعداد لا نهائية وبالتالي لا يمكن تحديد أكبر عدد أولي.

تطبيقات الأعداد الأولية:

لمدة طويلة، اعتبرت نظرية الأعداد بشكل عام ودراسة الأعداد الأولية بشكل خاص جزءا من الرياضيات البحتة، بدون أية تطبيقات باستثناء الاهتمام الذي يوليه علماء الرياضيات إلى هذه الدراسة.

فعلى سبيل المثال، الباحثون في نظرية الأعداد من أمثال عالم الرياضيات البريطاني غودفري هارولد هاردي، كانو يفتخرون بعملهم في مجال ليس لديه تطبيقات عسكرية.

ولكن هاته النظرة تغيرت تمامًا في سبعينات القرن العشرين، حين أعلن للعموم أن الأعداد الأولية قد تستعمل قاعدة لبناء خوارزميات التشفير باستخدام المفتاح المعلن، كما تُستعمل الأعداد الأولية أيضا في مولدات الأعداد شبه العشوائية.

أسئلة حول الأعداد الأولية:

مثال 1: أي من العددين عدد أولي، 13 أم 15؟

الإجابة:

يقبل الرقم 15 القسمة على أكثر من عاملين: 1 و 3 و 5 و 15. لذا فهو عدد غير أولي. من ناحية أخرى، العدد 13 يقبل القسمة على عاملين فقط: 1 و 13. ومن ثم فهو عدد أولي.